The Role of Linearity in AI: Decision Boundaries and Dynamical Systems
You’ve probably heard the phrase, “an eye for an eye, a tooth for a tooth.” This ancient principle, known as Lex Talionis from the Codex Hammurabi, is all about proportionality in justice. While it might evoke images of ancient Babylonian dentists struggling with retribution, it also sets the stage for an important topic in the world of artificial intelligence: linearity.
Linearity: A Blueprint for Understanding
In the past, this law wasn’t just a call for revenge but a way to promote a regulated form of justice. It aimed to keep violence at bay by ensuring that every crime resulted in an equivalent response—kind of like a mathematical equation. Imagine living in a world where every action had a predictable outcome and everything could be solved like algebra: simple, clear, and orderly.
For instance, consider Newton’s Third Law: “For every action, there is an equal and opposite reaction.” This principle reflects the essence of linearity, where understanding the world is straightforward and rooted in predictable patterns. In ideal worlds, everything balances out, and chaos becomes a thing of the past.
Moving Beyond Simplicity
However, reality paints a different picture. Our lives are filled with disproportionate responses and complexities that linear frameworks can’t always capture. Remember the Defenestration of Prague, a seemingly trivial act that ignited the Thirty Years’ War? Such events remind us that human behavior—much like the various components of AI—is often anything but linear.
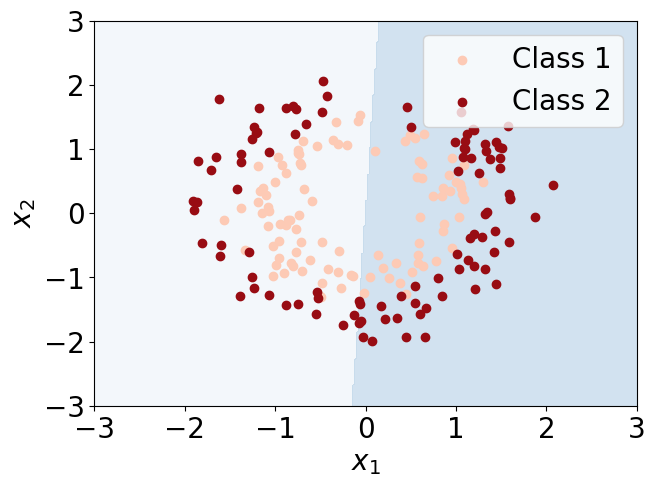
The Integral Role of Linearity in AI
So, why does this concept matter for AI enthusiasts? Decision boundaries, embeddings, and dynamical systems rely heavily on linear principles. These elements become foundational in developing next-gen Language Learning Models (LLMs) that not only predict outcomes but also learn and adapt based on user interactions.
-
Decision Boundaries: In supervised learning, linear classifiers create decision boundaries to separate different classes. These lines help machines discern between various types of data, whether it’s a cat or a dog or predicting whether you’d like a certain movie based on past preferences.
-
Embeddings: While it might sound technical, embedding involves converting data into a lower-dimensional space where relationships are maintained. A common example is using word embeddings in LLMs, where similarity in meaning can be represented as proximity in a mathematical space.
- Dynamical Systems: These systems study how variables evolve over time, crucial in developing models that can predict behavior based on previous actions. This dynamic nature is essential for technologies like recommendation systems that adapt in real-time.
Real-Life Implications and Future Outlook
AI models infused with linear principles help make sense of the vast complexities of data streams. Imagine walking through a busy city like Chicago during a summer festival, where thousands of pathways intertwine. If you were armed with a guide that emphasized clear, linear routes, navigating that chaos could become much simpler. That’s the power of understanding linearity within AI—guiding us through the labyrinth of information.
With AI continually evolving, it’s essential to recognize the blend of linear perspectives with more complex approaches. While linear models form the basis of many systems, the future lies in hybrid methods that embrace both order and chaos, offering us a more rounded understanding of AI capabilities.
Conclusion
In our exploration of AI and the critical role of linearity, we’ve unearthed a crucial element that governs decision-making and system dynamics. Understanding how linear systems affect AI processes invites us to think more deeply about their implications for the future.
The AI Buzz Hub team is excited to see where these breakthroughs take us. Want to stay in the loop on all things AI? Subscribe to our newsletter or share this article with your fellow enthusiasts!