Understanding Markov Decision Processes: A Practical Approach
Markov Decision Processes (MDPs) are crucial in the worlds of robotics and artificial intelligence, providing a foundation for advanced concepts like Reinforcement Learning and Partially Observable MDPs. While many resources tend to illustrate MDPs through theoretical "grid world" scenarios, these examples may lack relevance to real-world applications. If you’re keen to grasp the practical implications of MDPs, especially through relatable examples, you’re in the right place!
MDPs in Action: The Sandwich-Building PR2 Robot
Let’s dive into a real-life scenario featuring the PR2 robot—a popular research platform known for its versatility. Imagine the PR2 robot tasked with making a sandwich. This scenario is a perfect representation of an MDP because it involves various states (like the robot’s position, the availability of ingredients, and whether the sandwich is complete) and actions (like picking up an ingredient or placing it on the sandwich).
What Is an MDP?
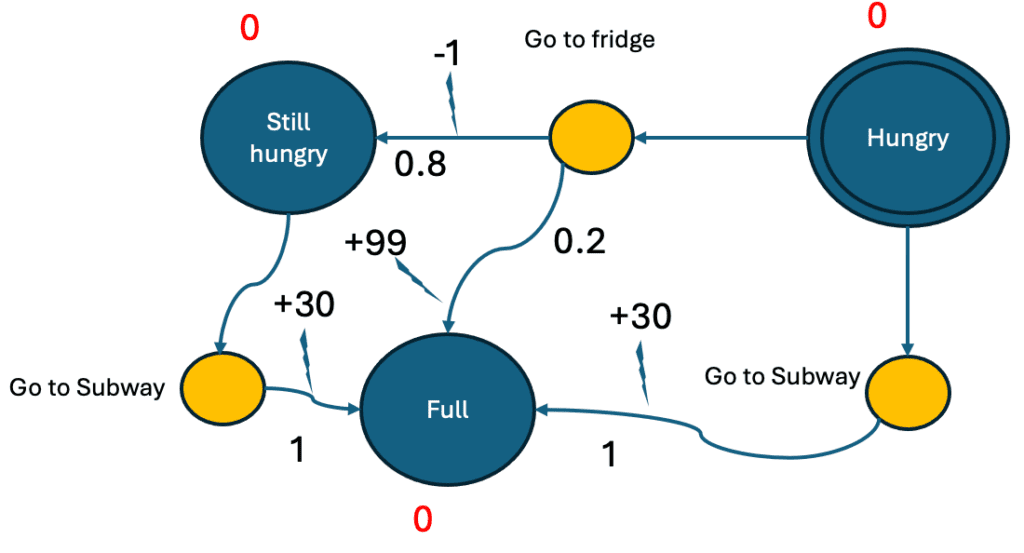
At its core, an MDP provides a mathematical framework for modeling decision-making in situations where outcomes are partly random and partly under the control of a decision-maker. In our sandwich-making robot example, the robot must choose the most effective action (like retrieving bread, lettuce, or tomato) based on the current state of its environment.
The Bellman Equation: A Guide for Decision-Making
The Bellman equation is fundamental when working with MDPs. It essentially defines the relationship between the value of a certain state and the values of its successor states. In simpler terms, to determine the best action at any given state, you need to consider not only the immediate rewards but also the potential future states derived from that action.
Let’s think about it in the context of our PR2 robot: if it’s currently holding the bread, it needs to evaluate whether picking up the lettuce next yields a better outcome than picking up the tomato. So, the robot uses the Bellman equation to assess the long-term value of each potential path to completing the sandwich.
Value Iteration: Calculating the Best Path
Value iteration is an algorithm used to compute the optimal policy for an MDP. It works by iteratively updating the value of each state until the values converge to their optimal levels. Essentially, with each iteration, the robot refines its understanding of which actions lead to the best rewards.
For the PR2 robot, through value iteration, it learns the best sequence of actions to build the perfect sandwich—optimizing its movements, selecting the right ingredients in the most efficient order, and minimizing the time it takes to complete its task.
Putting Theory into Practice: A Simple Python Implementation
To practically apply these concepts, you can implement a basic MDP model using Python. Here’s a quick outline of what that could look like:
- Define States: Create a list of states representing various positions and ingredient availability.
- Define Actions: Outline possible actions the robot can take.
- Set Up Rewards: Assign rewards based on the outcomes of each action.
- Implement the Bellman Equation: Use it to update the values of each state.
- Run Value Iteration: Loop through and optimize until convergence.
By translating these theoretical components into code, you can witness firsthand how MDPs drive intelligent decision-making—exactly as our PR2 robot does in the sandwich-making process.
Conclusion
Markov Decision Processes bridge the gap between abstract theory and practical implementation in robotics and AI. By using relatable examples like the PR2 robot making a sandwich, we can understand how MDPs, the Bellman equation, and value iteration contribute to effective decision-making in real-world applications.
The AI Buzz Hub team is excited to see where these breakthroughs take us. Want to stay in the loop on all things AI? Subscribe to our newsletter or share this article with your fellow enthusiasts.