Distinguishing Between Two Regression Models: A Guide to Statistical Significance

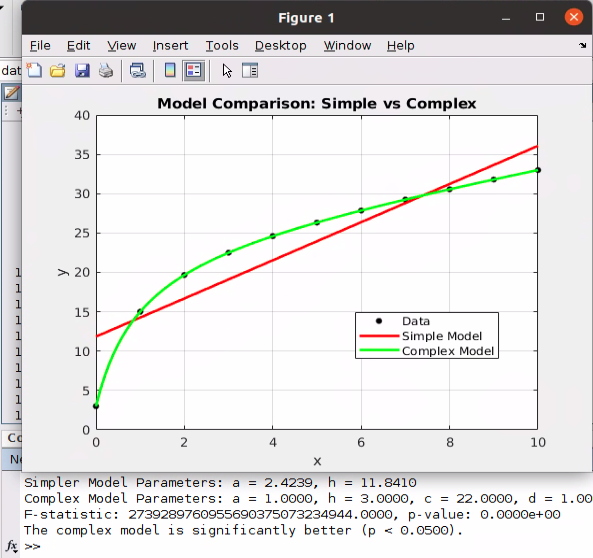
Understanding the F-test for Nested Models: Algorithms, Examples, and Implementation

When diving into the world of data analysis, many of us find ourselves comparing regression models to identify which one aligns best with our dataset. Often, this involves evaluating a simpler model against a more complex one that includes extra parameters. But here’s the thing: while a more complicated model may seem appealing, it doesn’t necessarily mean it’s a better fit. Sometimes, adding parameters can lead to overfitting, where the model captures noise in the data rather than the underlying trend.

So, how do we determine if that extra complexity is worth it? Enter the F-test for nested models. This statistical method allows us to assess whether the improvement in fit—measured by a reduction in Residual Sum of Squares (RSS)—is genuine or simply a fluke of chance.

What is the F-test for Nested Models?

In basic terms, the F-test helps us evaluate if a more complex model significantly improves prediction accuracy over a simpler model. We essentially want to know if the decrease in error (RSS) is statistically meaningful. If it is, we can justify using the more intricate model.

A Step-by-Step Algorithm

Here’s a straightforward algorithm for conducting the F-test for nested models:

Fit Both Models: Start by fitting your simpler (nested) model and your more complex model to your data.
Calculate RSS: Compute the Residual Sum of Squares for both models (RSS1 for the simpler model and RSS2 for the complex model).
Determine Degrees of Freedom: Identify the degrees of freedom for both models. This is crucial for calculating the F statistic.
Calculate the F Statistic: Use the formula:
[
F = \frac{(RSS1 – RSS2) / (df1 – df2)}{RSS2 / df2}
]
Where (df1) and (df2) are the degrees of freedom for the simpler and complex models, respectively.
Consult F-distribution Tables: To conclude, see if the computed F statistic exceeds the critical value from the F-distribution table for your chosen significance level (commonly 0.05).

Technical Implementation in MATLAB

For those who are tech-savvy, here’s a simple pseudocode followed by actual MATLAB code to implement this test:

Pseudocode:

1. Load data
2. Fit simpler model
3. Compute RSS1
4. Fit complex model
5. Compute RSS2
6. Calculate degrees of freedom
7. Calculate F statistic
8. Compare with the critical F-value from tables

MATLAB Code:

data = load('your_data.mat');
simpleModel = fitlm(data, 'Response ~ Predictor1');
complexModel = fitlm(data, 'Response ~ Predictor1 + Predictor2 + Predictor3');

RSS1 = sum(residuals(simpleModel).^2);
RSS2 = sum(residuals(complexModel).^2);

df1 = simpleModel.DFE; % degrees of freedom for simple model
df2 = complexModel.DFE; % degrees of freedom for complex model

F_statistic = ((RSS1 - RSS2) / (df1 - df2)) / (RSS2 / df2);
critical_value = finv(0.95, df1 - df2, df2);

if F_statistic > critical_value
    disp('The complex model significantly improves fit.');
else
    disp('No significant improvement from the complex model.');
end

Real-Life Application

Imagine you’re a data analyst in a local wildlife conservation organization, and you’re trying to model the population growth of a certain endangered species. You start with a simple linear regression using just the time variable. However, you consider adding environmental factors like rainfall and temperature to see if they influence growth rates.

After implementing the F-test, you discover that adding environmental variables significantly improves your model. This insight not only bolsters your analysis but also guides conservation efforts with actionable data.

Conclusion

In the realm of statistical modeling, the F-test for nested models is a powerful tool for decision-making. It not only reveals whether complexity adds value but also enhances the robustness of your predictions. If you’re keen on incorporating the F-test in your analyses, now’s the time to roll up your sleeves and dive into the provided MATLAB code.

The AI Buzz Hub team is excited to see where these breakthroughs take us. Want to stay in the loop on all things AI? Subscribe to our newsletter or share this article with your fellow enthusiasts.

What's Hot